Como consecuencia matemática de las ecuaciones de Maxwell y además con el objetivo de simplificar sus cálculos se han introducido los conceptos de potencial vector (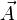
) y potencial escalar (
). Este potencial vector no es único y no tiene significado físico claro pero se sabe que un elemento infinitesimal de corriente da lugar a una contribución 
paralela a la corriente.13 Este potencial se obtiene como consecuencia de la ley de Gauss para el flujo magnético, ya que se conoce que si la divergencia de un vector es cero, ese vector como consecuencia define a un rotacional, así:14
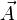) y potencial escalar (). Este potencial vector no es único y no tiene significado físico claro pero se sabe que un elemento infinitesimal de corriente da lugar a una contribución paralela a la corriente.13 Este potencial se obtiene como consecuencia de la ley de Gauss para el flujo magnético, ya que se conoce que si la divergencia de un vector es cero, ese vector como consecuencia define a un rotacional, así:14
A partir de este potencial vector y de la ley de Faraday puede definirse un potencial escalar así:12
donde el signo menos ( − ) es por convención. Estos potenciales son importantes porque poseen una simetría gauge que nos da cierta libertad a la hora de escogerlos.12 El campo eléctrico en función de los potenciales:
Hallamos que con la introducción de estas cantidades las ecuaciones de Maxwell quedan reducidas solo a dos, puesto que, la ley de Gauss para el campo magnético y la ley de Faraday quedan satisfechas por definición. Así la ley de Gauss para el campo eléctrico escrita en términos de los potenciales:
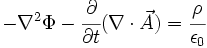
Nótese que se ha pasado de un conjunto de cuatro ecuaciones diferenciales parciales de primer orden a solo dos ecuaciones diferenciales parciales pero de segundo orden. Sin embargo, estas ecuaciones se pueden simplificar con ayuda de una adecuada elección del gauge.
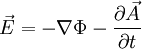
No hay comentarios:
Publicar un comentario