En la relatividad especial, las ecuaciones de Maxwell en el vacío se escriben mediante unas relaciones geométricas, las cuales toman la misma forma en cualquier sistema de referencia inercial. Éstas están escritas en términos de cuadrivectores y tensores contravariantes, que son objetos geométricos definidos en M4. Estos objetos se relacionan mediante formas diferenciales en relaciones geométricas que al expresarlas en componentes de los sistemas coordenados Lorentz proporcionan las ecuaciones para el campo electromagnético.
La cuadricorriente  está descrita por una 1-forma y lleva la información sobre la distribución de cargas y corrientes. Sus componentes son:
está descrita por una 1-forma y lleva la información sobre la distribución de cargas y corrientes. Sus componentes son:
 está descrita por una 1-forma y lleva la información sobre la distribución de cargas y corrientes. Sus componentes son:
está descrita por una 1-forma y lleva la información sobre la distribución de cargas y corrientes. Sus componentes son:Que debe cumplir la siguiente relación geométrica para que se cumpla la ecuación de continuidad.
Escrito en componentes de los sistemas coordenados Lorentz queda:
Para poner en correspondencia objetos del mismo rango, se utiliza el operador de Laplace-Beltrami o laplaciana definida como:
Podemos poner en correspondencia el cuadrivector densidad de corriente con otro objeto del mismo rango como es el cuadripotencial, que lleva la información del potencial eléctrico y el potencial vector magnético.
O escrito en coordenadas Lorentz obtenemos que:
Expresión que reproduce las ecuaciones de onda para los potenciales electromagnéticos.
La 1-forma A lleva la información sobre los potenciales de los observadores inerciales siendo sus componentes:
Para obtener el objeto geométrico que contiene los campos, tenemos que subir el rango de A mediante el operador diferencial exterior 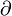 obteniendo la 2-forma F campo electromagnético. En forma geométrica podemos escribir:
obteniendo la 2-forma F campo electromagnético. En forma geométrica podemos escribir:
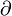 obteniendo la 2-forma F campo electromagnético. En forma geométrica podemos escribir:
obteniendo la 2-forma F campo electromagnético. En forma geométrica podemos escribir:Que expresado para un sistema inercial Lorentz tenemos que:
Con lo que obtenemos el tensor de campo electromagnético.
[editar]Primer par de ecuaciones de Maxwell
La siguientes expresiones ligan los campos con las fuentes, relacionamos la cuadricorriente con el tensor campo electromagnético mediante la forma geométrica:
O bien en coordenadas Lorentz:
[editar]Obtención de las ecuaciones
Para un observable en S partiendo de expresión en coordenadas Lorentz podemos obtener:
- Para
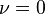 tenemos que:
tenemos que:  , entonces:
, entonces:
Por tanto:
- Para
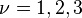 podemos obtener de la misma forma que:
podemos obtener de la misma forma que:
[editar]Segundo par de ecuaciones de Maxwell
Corresponden a las ecuaciones homogéneas. Escritas en forma geométrica tenemos que:
Que corresponde con la expresión en los sistemas coordenados Lorentz:
Donde el tensor  es el tensor dual de F. Se obtiene mediante el operador de Hodge.
es el tensor dual de F. Se obtiene mediante el operador de Hodge.
 es el tensor dual de F. Se obtiene mediante el operador de Hodge.
es el tensor dual de F. Se obtiene mediante el operador de Hodge.[editar]Obtención de las ecuaciones
- Para
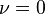 :
:
Por tanto:
- Para
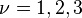 se obtiene la ecuación vectorial:
se obtiene la ecuación vectorial:
La propiedad 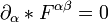 reproduce las ecuaciones de Maxwell internas, que se puede expresar como
reproduce las ecuaciones de Maxwell internas, que se puede expresar como  , que se puede escribir en los sistemas coordenados Lorentz como:
, que se puede escribir en los sistemas coordenados Lorentz como:
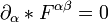 reproduce las ecuaciones de Maxwell internas, que se puede expresar como
reproduce las ecuaciones de Maxwell internas, que se puede expresar como  , que se puede escribir en los sistemas coordenados Lorentz como:
, que se puede escribir en los sistemas coordenados Lorentz como: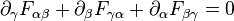
Forma Geométrica Covariante Lorentz Descripción 
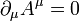
Condición/gauge de Lorenz (*) 

Definición de Campos Electromagnéticos 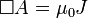

Ecuaciones de Ondas 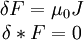
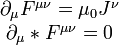
Ecuaciones de Maxwell 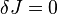
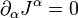
Ley de conservación de la Carga
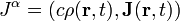
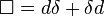



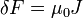

![\mu _0 c \rho (\mathbf{r},t)=\part_1 F^{1 0}+\part_2 F^{2 0}+\part_3 F^{3 0} =
\frac {1}{c} \left [ \frac{\part E_x}{\part x}+\frac{\part E_y}{\part y}+\frac{\part E_z}{\part z} \right ]](http://upload.wikimedia.org/math/9/f/a/9fa9d7fa7211b01d1ddba1dad161c870.png)
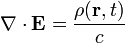

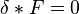
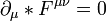
![\partial_\mu * F^{\mu 0}=\partial_1 * F^{1 0}+\partial_2 * F^{2 0}+\partial_3 * F^{3 0}=\left [ \frac{\part B_x}{\part x}+\frac{\part B_y}{\part y}+\frac{\partial B_z}{\part z} \right ]=0](http://upload.wikimedia.org/math/4/e/3/4e327ad914415b80b6dcdb5ecdb4bd6f.png)
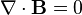
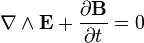
No hay comentarios:
Publicar un comentario